Is increasing ie. The curve is called the probability density function abbreviated as pdf.
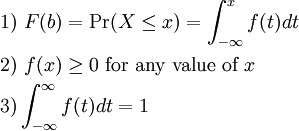
2 3 The Probability Density Function Math 105 Probability Module
To prove right continuity you need countable additivity.

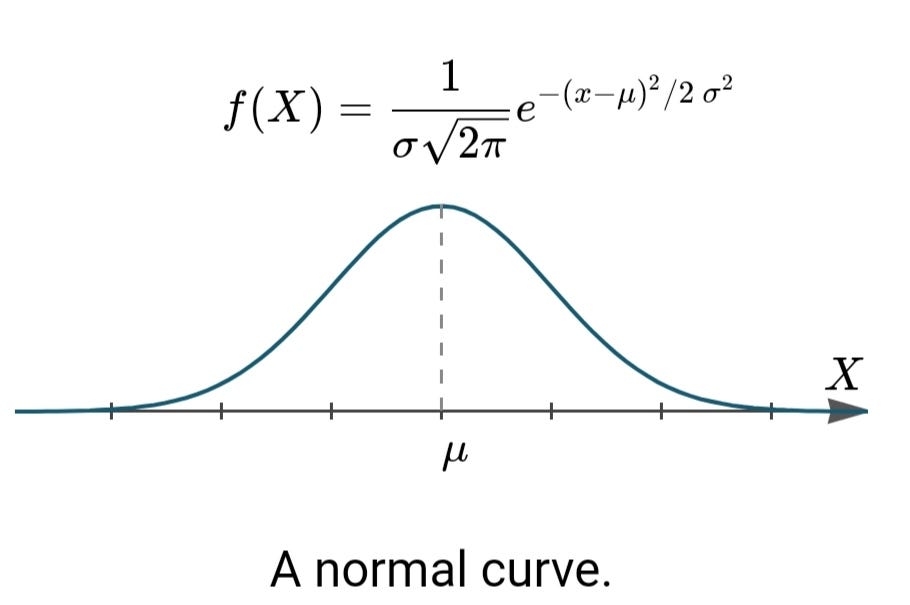
Probability distribution function properties. For example discrete distributions assign positive probability to intervals of length 0. Probability distribution of a continuous random variable if x is a discrete random variable with discrete values x 1 x 2 x n then the probability distribution function is f x p x x i. We use the density function fx to draw the graph of the probability distribution.
The probability assigned to an interval is certainly not bounded by its length. Below we will shortly discuss the most basic properties. Assume picking a card randomly from a deck of cards.
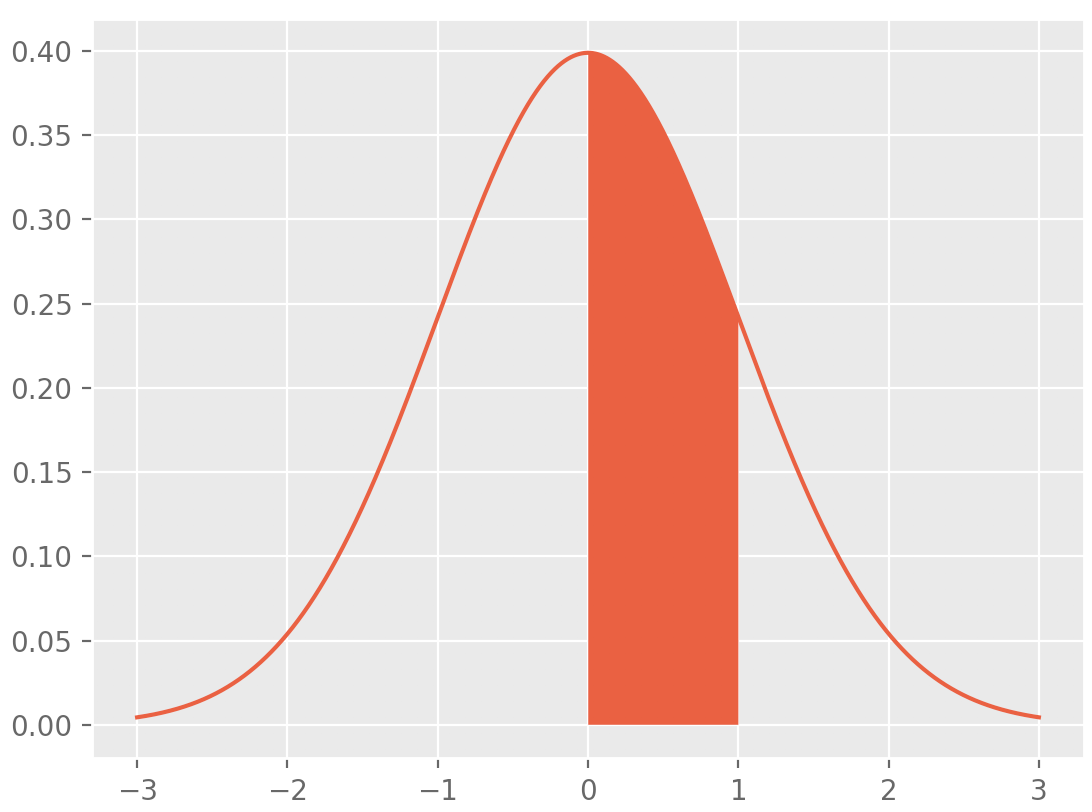
Namely that the probability between two outcomes lets say a and b is the integral of the probability density function between those two points this is equivalent to finding the area under the curve produced by the probability density function between the. Its distribution function is. If a random variable x has frequency function f x then the.
If g and h are independent then. Fx is the function that corresponds to the graph. Similar to the proof of property 1b of expectation.
The area under the curve between these values. Weve now seen another property of probability density functions. The cumulative distribution function is used to evaluate probability as area.
If a continuous random variable x has frequency function f x then the expected value of g x is. We use the symbol fx to represent the curve. If the events a b.
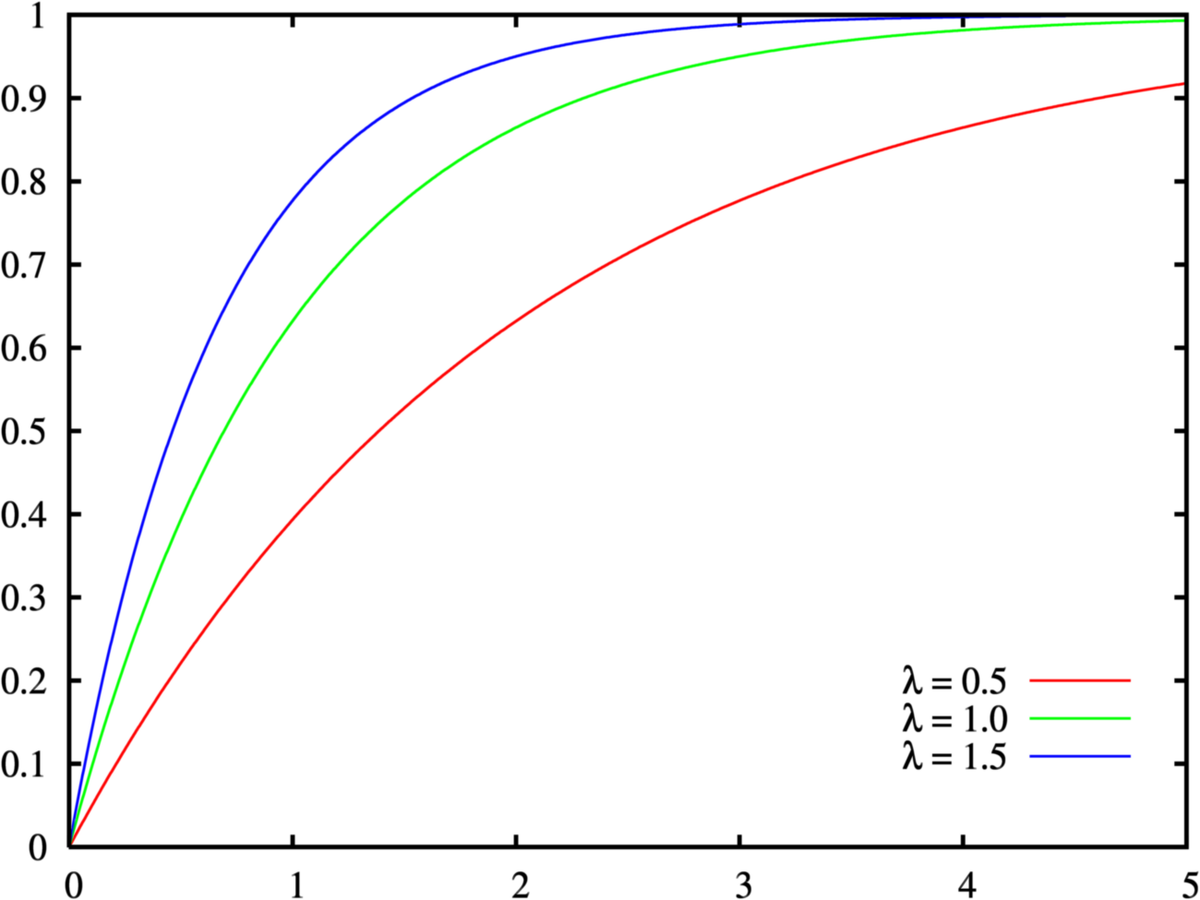
Every distribution function enjoys the following four properties. Advanced properties of probability distributions. Mathematically the cumulative probability density function is the integral of the pdf and the probability between two values of a continuous random variable will be the integral of the pdf between these two values.
Are mutually exclusive we have that p a b p a p b. Suppose a random variable can take only two values 0 and 1 each with probability 12. The distribution function for a continuoous random variable is f x x p x x i dx.
0 p a 1 a probability can never be larger than 1 or smaller than 0 by definition.
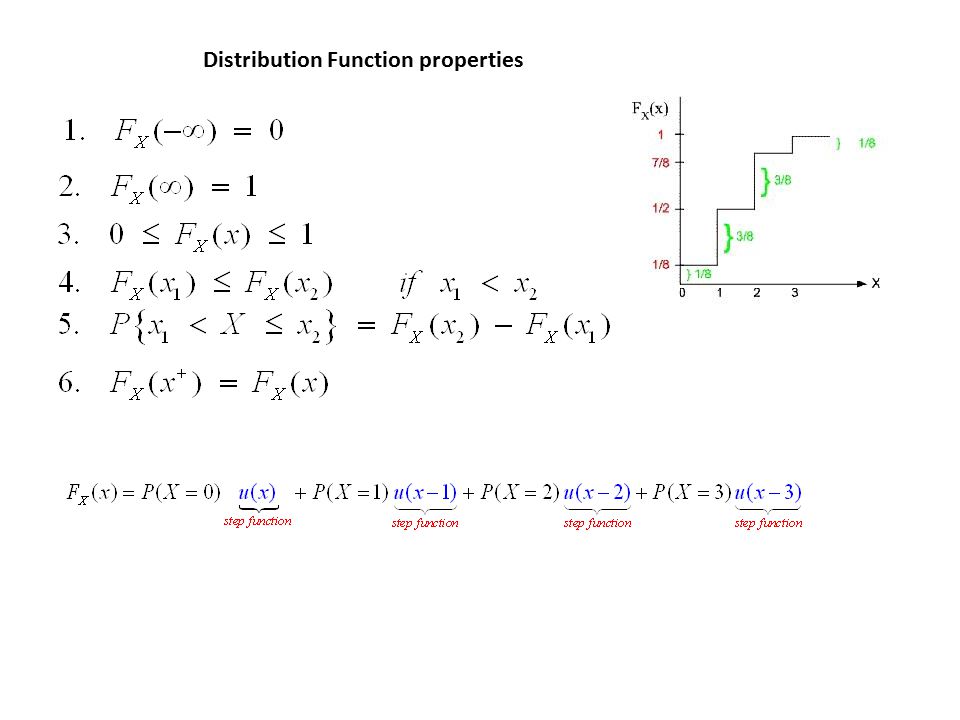
Distribution Function Properties Density Function We Define The Derivative Of The Distribution Function F X X As The Probability Density Function Ppt Download

One Random Variable Random Process Ppt Video Online Download

Probability Density Function Wikipedia

Solved 3 Density Functions A What Are The Two Propertie Chegg Com

Probability Distributions Ppt Video Online Download

Probability Distribution

Distribution Function And Its Properties
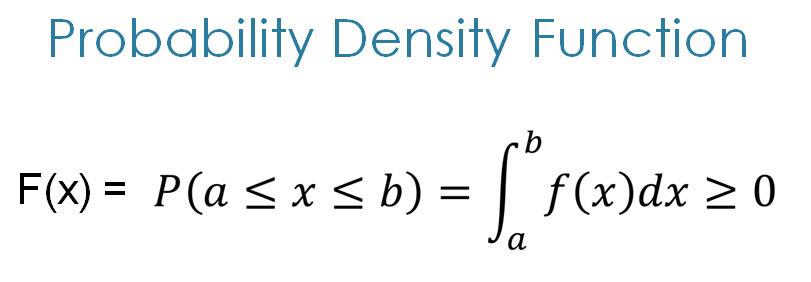
Continuous Probability Distributions Env710 Statistics Review Website

Continuous Probability Distribution Analytics Buddhu

Joint Probability Density Function Communication Analog And Digital Gate Ece Part 2 Unacademy

Probability Density Function

5 1 Two Discrete Random Variables Example Two Discrete Random Variables Figure 5 1 Joint Probability Distribution Of X And Y In Example Ppt Download

Understanding Probability Distributions Statistics By Jim

Probability Density Function Pdf

Probability Density Function Pdf Definition Formulas Example
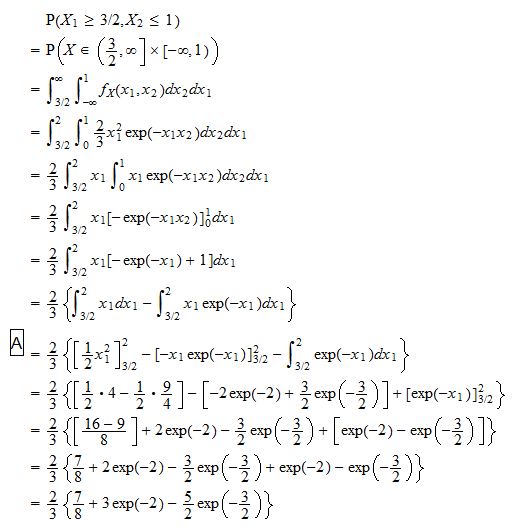
Joint Probability Density Function

Chap05 Continuous Random Variables And Probability Distributions

1 Engineering Computation Part 6 2 Probability Density Function Ppt Download

Solved 2 1 For Each Of The Functions Given Below Determi Chegg Com
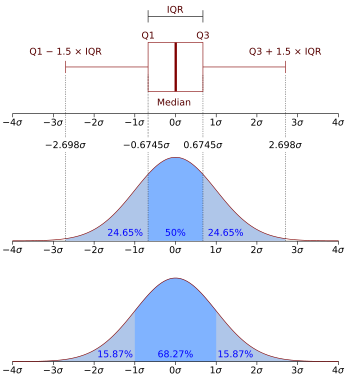
Probability Density Function Wikipedia

L05 3 Probability Mass Functions Youtube

Ppt Joint Probability Distribution Powerpoint Presentation Free Download Id 1587846

Theoretical Distributions In Probability And Statistics Ppt Download

Https Encrypted Tbn0 Gstatic Com Images Q Tbn And9gctpmb7ecyy2ahomhnkk4g4jx1vxzitxgj1og8ednyk22o3pjysm Usqp Cau

14 The Cumulative Distribution Function
Probability Density Function Pdf

Probability And Statistics For Computer Vision 101 Part 2 By Sho Nakagome Sho Jp Medium

Joint Probability Density Function Joint Pdf Properties Of Joint Pdf Joint Probability Distribution Youtube

Random Variable And Probability Distribution Ppt Video Online Download

Probability Concepts Explained Probability Distributions Introduction Part 3 By Jonny Brooks Bartlett Towards Data Science

Probability Density Function

Probability Concepts Explained Probability Distributions Introduction Part 3 By Jonny Brooks Bartlett Towards Data Science

Probability Density Function Wikipedia
Probability Density Functions Video Khan Academy

Engineering Made Easy Probability Density Function Pdf Definition Basics And Properties Of Probability Density Function Pdf With Derivation And Proof

A Gentle Introduction To Probability Density Estimation
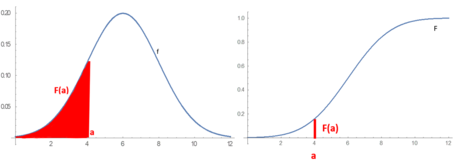
Probability Distribution Wikipedia

Understanding Probability Distributions Statistics By Jim
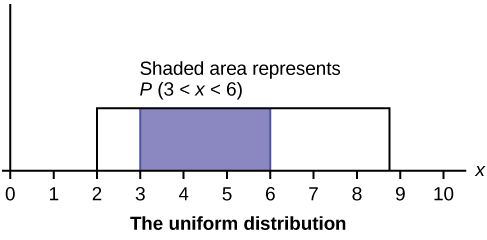
Properties Of Continuous Probability Density Functions Introductory Business Statistics

Prob 3 2 Properties Of Distribution Function Youtube

Https Faculty Math Illinois Edu Hildebr 370 408continuous Pdf

Probability Distribution Functions F Pdfs Of Six Baryonic Properties Download Scientific Diagram

Probability Density Function An Overview Sciencedirect Topics

Continuous And Discrete Probability Distributions Minitab Express

Probability Distribution Function Probability Density Function Properties Youtube
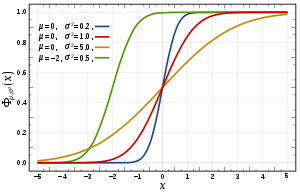
Cumulative Distribution Function Wikipedia

Content Cumulative Distribution Functions
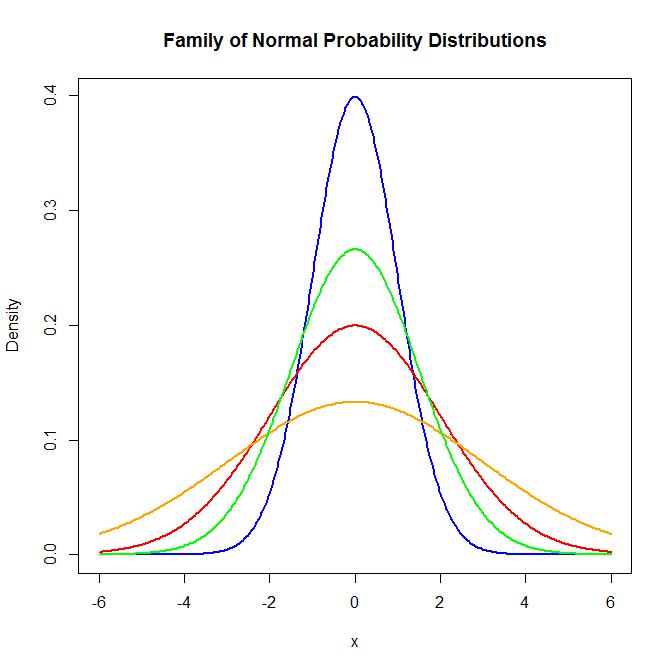
Continuous Probability Distributions Env710 Statistics Review Website

7 1 Properties Of The Normal Distribution

Probability Density Function

Understanding Probability Distributions Statistics By Jim

Lecture Notes 4 Continuous Probability Distributions Normal Distribution Probability Density Function

Solved 1 Write Two Differences Between Pdf And Pmf 2 S Chegg Com
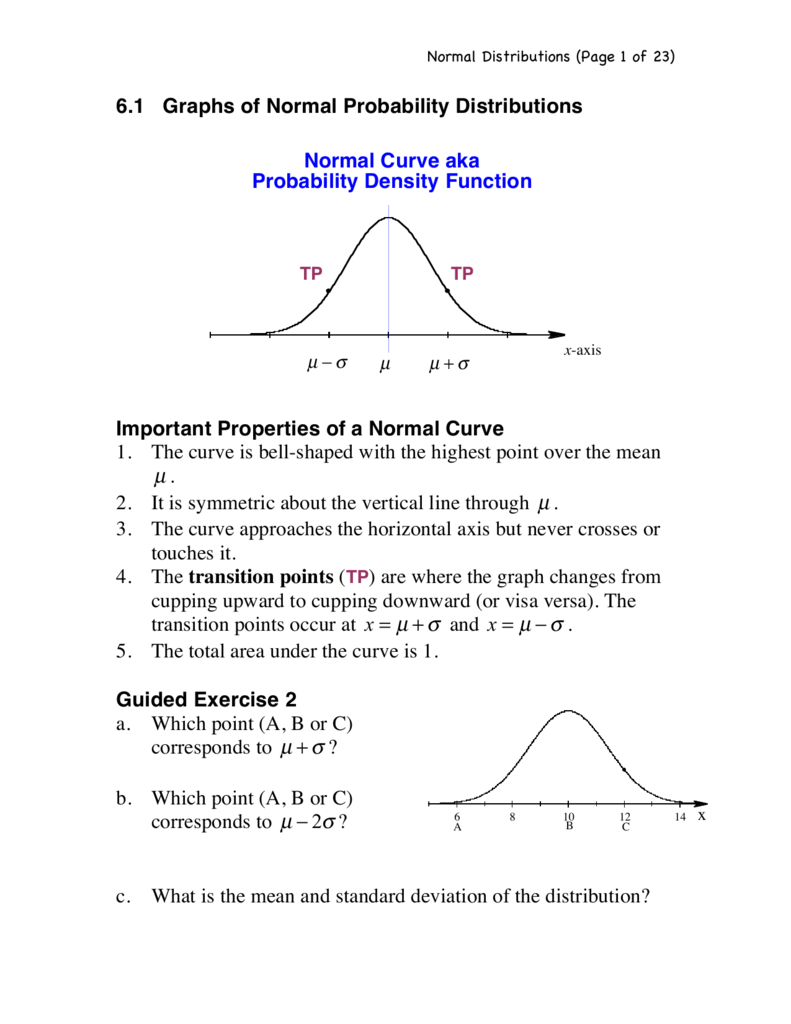
6 1 Graphs Of Normal Probability Distributions X Important Properties

Engineering Made Easy Probability Density Function Pdf Definition Basics And Properties Of Probability Density Function Pdf With Derivation And Proof
Probability Concepts Explained Probability Distributions Introduction Part 3 By Jonny Brooks Bartlett Towards Data Science
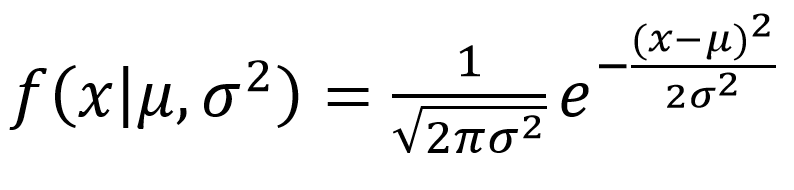
Tutorial Probability Distributions In Python Datacamp
Cumulative Distribution Function Wikipedia
Five Probability Distribution Every Data Scientist Should Learn By Keerti Prajapati Medium

Random Variables And Probability Distributions Pdf Free Download

Probability Density Function
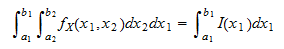
Joint Probability Density Function

Discrete Distributions Ppt Video Online Download
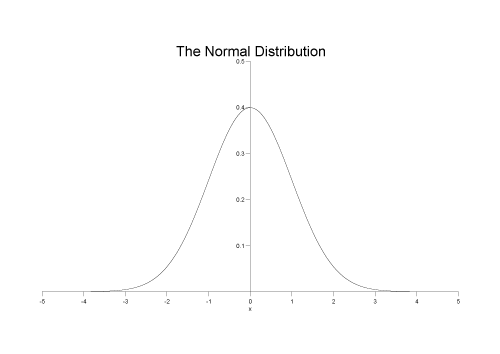
Non Member Properties 1 47 0

Solved The Cauchy Distribution Has A Probability Density Chegg Com
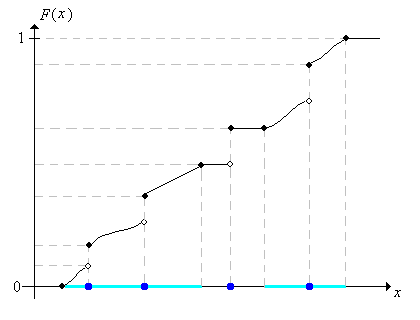
Distribution Functions

Ppt Joint Probability Distributions Powerpoint Presentation Free Download Id 639941
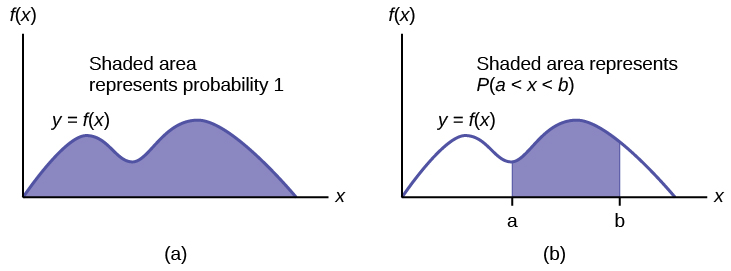
Properties Of Continuous Probability Density Functions Introductory Business Statistics
/dotdash_Final_Probability_Distribution_Sep_2020-01-7aca39a5b71148608a0f45691b58184a.jpg)
Probability Distribution Definition
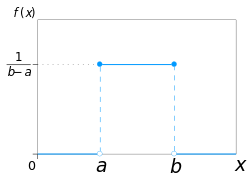
Continuous Uniform Distribution Wikipedia

Site Specific Probability Distribution Of Geotechnical Properties Sciencedirect
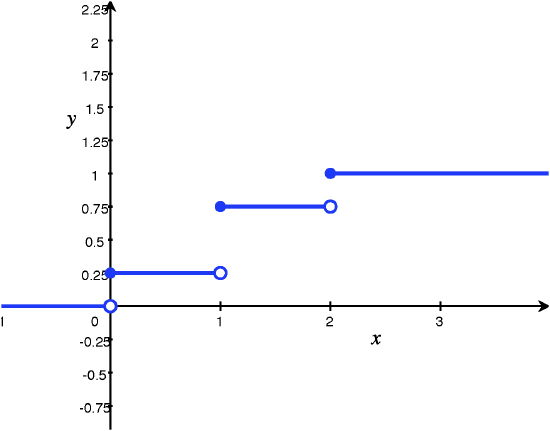
3 2 Probability Mass Functions Pmfs And Cumulative Distribution Functions Cdfs For Discrete Random Variables Statistics Libretexts

Https Encrypted Tbn0 Gstatic Com Images Q Tbn And9gcsfz1h S2pfrn41 Asxwnbgc64yxbb7sc Oqs0c Oyl W2w Gn Usqp Cau

Distribution Function And Its Properties

A Gentle Introduction To Probability Density Estimation

Solved Exercise 5 2 Consider The Random Variable X With C Chegg Com

Stat 515 Chapter 6 Continuous Distributions
Probability Distributions And Their Mass Density Functions

Joint Probability Distribution Wikipedia

Distribution Function And Its Properties

Doc A New Distribution L Probability Distribution Function Mohammad Miyan Academia Edu

Show That The Following Function Satisfies The Pro Chegg Com

Pdf Investigation On Probability Density Function For Cone Penetration Test Data
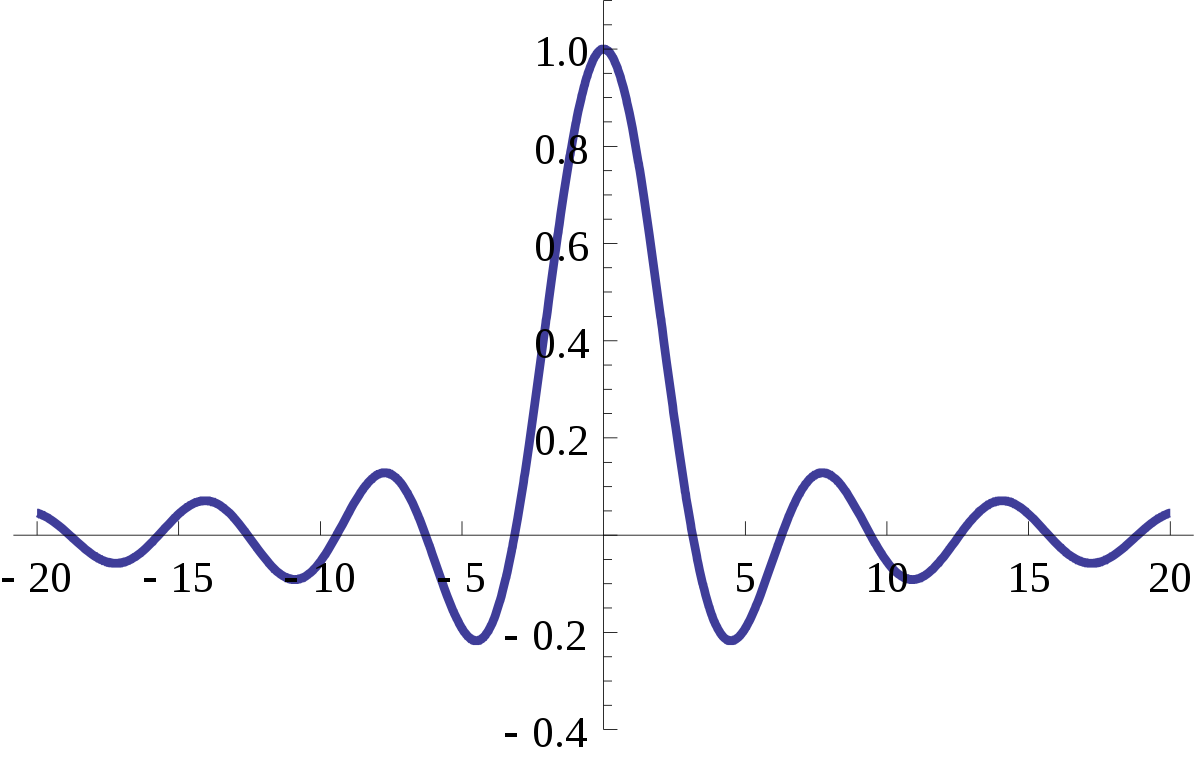
Characteristic Function Probability Theory Wikipedia

5 Joint Probability Distributions Chapter Outline Ppt Download

Ch7 Normaldistribution

Cumulative Distribution Function
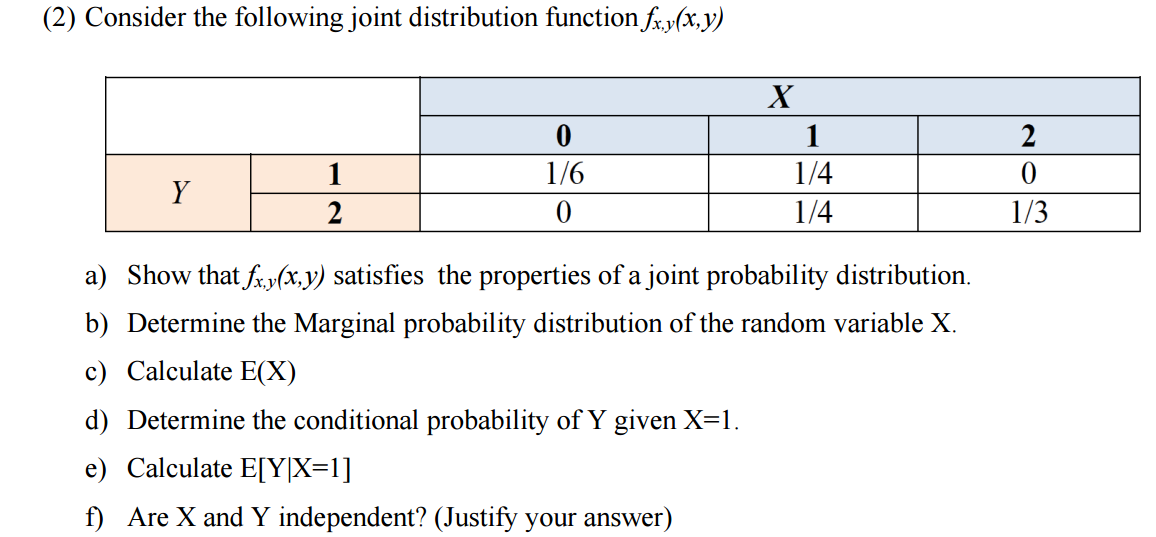
Solved Consider The Following Joint Distribution Function Chegg Com
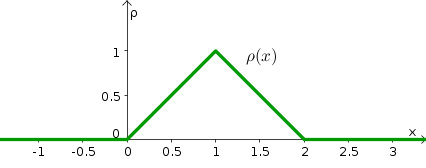
The Idea Of A Probability Density Function Math Insight

Pdf A New Skew Logistic Distribution And Its Properties

Joint Probability Distributions Ppt Download

Probability Distribution Wikipedia

Probability Density Functions An Overview Sciencedirect Topics
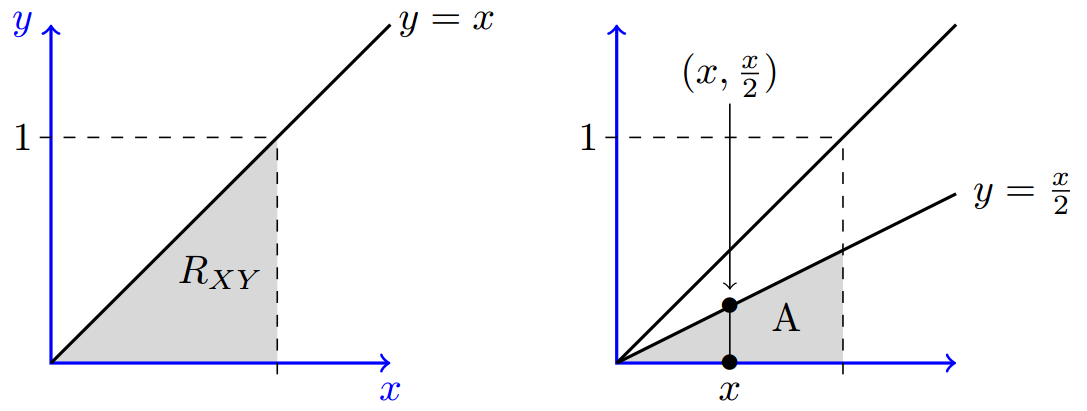
Joint Probability Density Function Joint Continuity Pdf

Mdm4u Continuous Probability Distributions

Https Content Sciendo Com Downloadpdf Journals Mjpaa 1 2 Article P70 Pdf

Properties Of The Probability Distribution Function Youtube

Https Encrypted Tbn0 Gstatic Com Images Q Tbn And9gcqcgwc Mbh Cbq2lplovz5pi8kt55tqxw9vjdmz4pr1gmuykh4t Usqp Cau

Copyright C Cengage Learning All Rights Reserved 8 Probability Distributions And Statistics Ppt Download

Probability Concepts Explained Probability Distributions Introduction Part 3 By Jonny Brooks Bartlett Towards Data Science
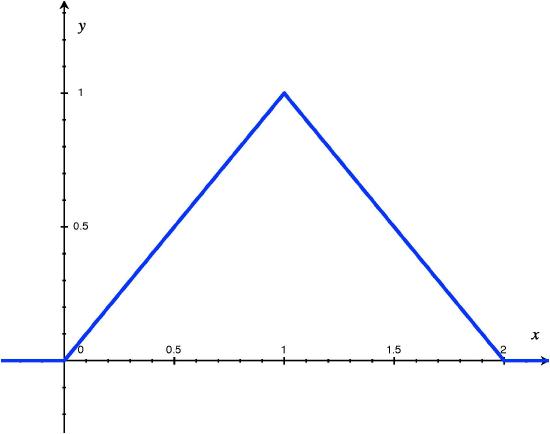
4 1 Probability Density Functions Pdfs And Cumulative Distribution Functions Cdfs For Continuous Random Variables Statistics Libretexts
/close-up-of-stock-market-data-1158402857-2139dd8ca4154f4496b11684cd2de6a2.jpg)
Probability Density Function Pdf Definition













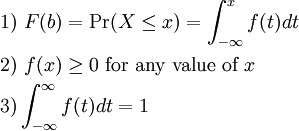





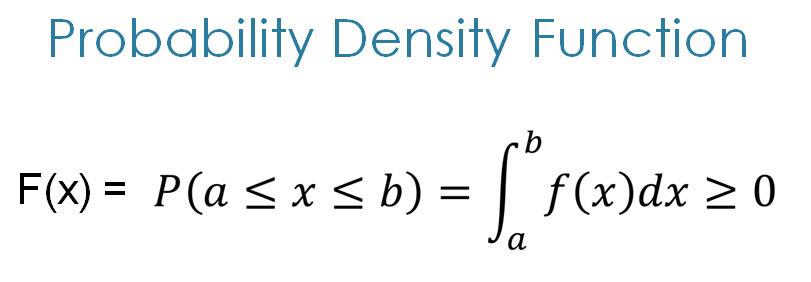




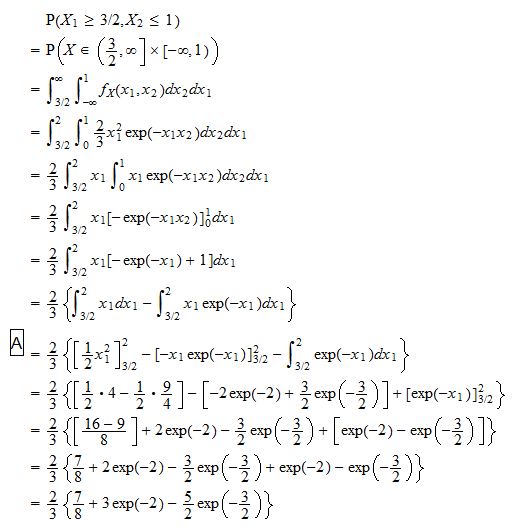



























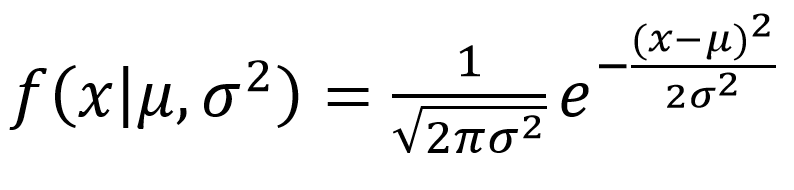



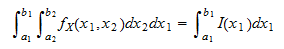






/dotdash_Final_Probability_Distribution_Sep_2020-01-7aca39a5b71148608a0f45691b58184a.jpg)























/close-up-of-stock-market-data-1158402857-2139dd8ca4154f4496b11684cd2de6a2.jpg)
Post a Comment for "Probability Distribution Function Properties"